( Idéas aportadas por Joan Marqués y Pere Joan Planes)

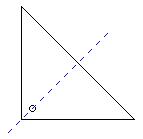
Este segundo método, a diferencia del de Villard de Honnecourt no necesita de ayudantes, únicamente hay que construír un triangulo equilátero de cartón o madera. Sobre la línea de su perpendicular , en el lado del ángulo recto, es decir, del de 90° ,taladramos un agujero. El triangulo así preparado se fija a un palo con un clavo de diámetro lígeramente inferior al agujero taladrado, de manera que quede suelto, por lo que por su propio peso se nivelará. al tener el mísmo peso a ambos lados.

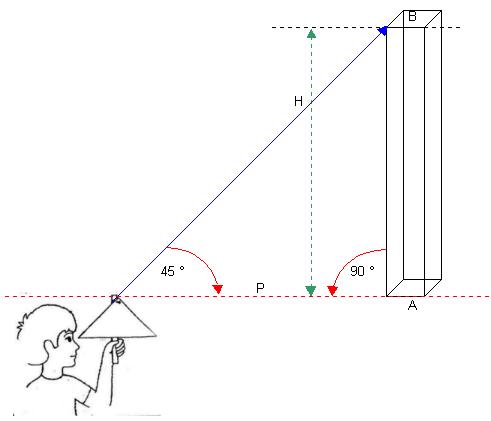
Nos situamos sobre una línea imaginaria P, paralela a la torre que queremos medir y nos movemos adelante y atrás hasta hacer coincidir la altura con la línea que marca el cateto. La distancia desde nosotros al pie de la torre es la mísma que la altura del edificio.

Para no tener que agacharnos, podemos marcar la medición a partir de la altura de nuestros ojos, que marcaremos en el edificio. Una vez efectuada la medición, únicamente hay que sumarle esta altura para saber la altura total.

Naturalmente, ambos métodos son aproximados, no porque el método no sea exacto, que lo es, sino por los instrumentos utilizados. Con instrumentos de precisión de geógrafo, (como los que vemos midiendo en las carreteras) se calcula la distancia con una precisión de 1 centímetro.

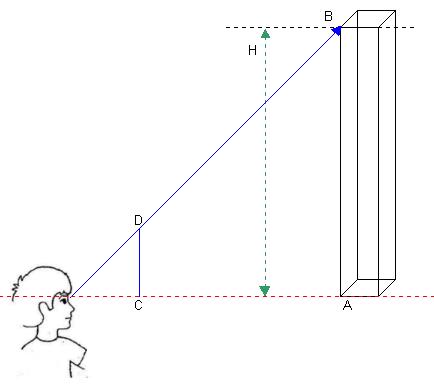
Un tercér método consiste en la aplicació del teorema de Tales : Si conocemos la longitud C-A y la altura C-D podemos conocer la altura A-B. A la hora de calcular hay que recordar de sumar a C-A la distancia que vá desde el ojo hasta C ; que llamaremos E.
El cálculo es simplemente una regla de tres:
si EC = DC ; entonces EA = x

Ver escuadras
Ver Villard de Honencourt:( método medieval para calcular la altura de un edificio )